算法的时间与空间复杂度详解

Posted on Edited on In Views:

1 概述

算法（Algorithm）是指用来操作数据、解决程序问题的一组方法。对于同一个问题，使用不同的算法，也许最终得到的结果是一样的，但在过程中消耗的资源和时间却会有很大的区别。

那么应该如何去衡量不同算法之间的优劣呢？

一般是从算法程序占用的时间和空间两个维度去衡量：

  • 时间维度：是指执行算法所消耗的时间，一般用时间复杂度来描述；
  • 空间维度：是指执行算法所需要占用的内存空间，一般用空间复杂度来描述；

因此评价算法效率优劣一般是看它的时间复杂度与空间复杂度情况。而这两者无法兼得，需要用户从中找出一个平衡点。

接下来记录下如何计算算法的时间复杂度与空间复杂度。

2 时间复杂度

一般在代码运行中统计一个程序运行耗时，可以通过代码的时间埋点，然后将代码执行一遍，就可统计出程序的实际耗时。那么如此是否可以用来计算算法的时间复杂度？

其实是可以的。但是这不能用来作为抽象的、统一标准的计算方法。因为其中有非常多的变量，如程序的运行环境的差距（配置高的机器与配置低的机器对于相同的代码运行速度也有非常大的差距）、如算法执行的数据量（数据规模大小对算法执行速度的影响也非常大）。

因此，我们使用一种更为通用的、抽象的方法：大 O 符号表示法，即 T(n) = O(f(n))

例子：

1
2
3
4
5
for(i=1; i<=n; ++i)
{
   j = i;
   j++;
}

通过大 O 符号表示法 ，这段代码的时间复杂度为：O(n) ，如何计算？

在大 O 符号表示法中，时间复杂度的公式是： T(n) = O(f(n))，其中 f(n) 表示每行代码执行次数之和，而 O 表示正比例关系，这个公式的全称是：算法的渐进时间复杂度。

继续看上面的例子，假设每行代码的执行时间都是一样的，我们用一个单位时间来表示，那么这个例子的第一行耗时是一个单位时间，第三行的执行时间是 n 个单位时间，第四行的执行时间也是 n 个单位时间（第二行和第五行是符号，暂时忽略），那么总时间就是一个单位时间 + n 个单位时间 + n 个单位时间 ，即 (1+2n) 个单位时间，即：T(n) = (1+2n)个单位时间，从这个结果可以看出，这个算法的耗时是随着 n 的变化而变化，因此，我们可以将这个算法的时间复杂度简化为：T(n) = O(n)

重点解释下为何可以简化？
如上所述，大 O 符号表示法描述的是算法渐进时间复杂度，表示的代码执行时间的增长变化趋势，而不是真实的代码的具体执行时间。
在例子中的 T(n) =Time (1+2n), 当 n 趋于无限大时，其中的常量 1 与倍数 2 都没有意义了。所以可以直接简化为 T(n) = O(n)

常见的时间复杂度：

  • 常数阶 O (1)
  • 对数阶 O (logN)
  • 线性阶 O (n)
  • 线性对数阶 O (nlogN)
  • 平方阶 O (n²)
  • 立方阶 O (n³)
  • K 次方阶 O (n^k)
  • 指数阶 (2^n)

复杂度的顺序为：

O(1) < O(logN) < O(n) < O(nlogN) < O(n²) < O(n³) < O(n^k) < (2^n)

时间复杂度越来越大，执行的效率越来越低

2.1 常数阶 O (1)

无论代码执行了多少行，只要是没有循环等复杂结构，那这个代码的时间复杂度就都是 O(1)，如：

1
2
3
4
5
int i = 1;
int j = 2;
++i;
j++;
int m = i + j;

上述代码在执行的时候，它消耗的时候并不随着某个变量的增长而增长，那么无论这类代码有多长，即使有几万几十万行，都可以用 **O (1)** 来表示它的时间复杂度。

2.2 对数阶 O (logN)

1
2
3
4
5
int i = 1;
while(i<n)
{
    i = i * 2;
}

如上代码，在 while 循环里面，每次都将 i 乘以 2，得到结果 i 距离 n 就越来越近了。假设循环 x 次之后，i 就大于 n，此时这个循环就退出了，也就是说 2 的 x 次方大于等于 n，那么 x = log2^n

也就是说当循环 log2^n 次后，这个代码的 while 循环就结束了。因此这个代码的时间复杂度为：O(logn)

2.3 线性阶 O (n)

与开始头的例子一致

1
2
3
4
5
for(i=1; i<=n; ++i)
{
   j = i;
   j++;
}

这段代码，for 循环里面的代码会执行 n 遍，因此它消耗的时间是随着 n 的变化而变化的，因此这类代码都可以用 **O (n)** 来表示它的时间复杂度。

2.4 线性对数阶 O (nlogN)

线性对数阶 O(nlogN) 其实是将时间复杂度为 O(logn) 的代码循环 n 遍，那么它的时间复杂度就是 n * O(logN)，也就是 **O (nlogN)**。如：

1
2
3
4
5
6
7
8
for(m=1; m<n; m++)
{
    i = 1;
    while(i<n)
    {
        i = i * 2;
    }
}

2.5 平方阶 O (n²)

平方阶 O(n²) 就更容易理解了，把 O(n) 的代码再嵌套循环一遍，它的时间复杂度就是 **O (n²) **。如：

1
2
3
4
5
6
7
8
for(x=1; i<=n; x++)
{
   for(i=1; i<=n; i++)
    {
       j = i;
       j++;
    }
}

2.6 立方阶 O (n³) & K 次方阶 O (n^k)

参考上面的 O (n²) 去理解，O (n³) 相当于三层 n 循环，其它的类似。

2.7 指数阶 (2^n)

1
2
3
4
5
6
7
8
9
int fib(int n)
{
    if (n <= 0)    //基本情况
        return 0;
    else if (n == 1) // 基本情况
        return 1;
    else
        return fib(n - 1) + fib(n - 2);
}

以上代码为斐波那契数列
显然运行次数，T(0) = T(1) = 1，同时 T(n) = T(n - 1) + T(n - 2) + 1，这里的 1 是其中的加法算一次执行。通过归纳证明法可以证明，当 n >= 1 时 T(n) < (5/3)^n，同时当 n > 4 时 T(n) >= (3/2)^n，简化后为 O(2^n)

2.8 常用排序算法时间复杂度统计

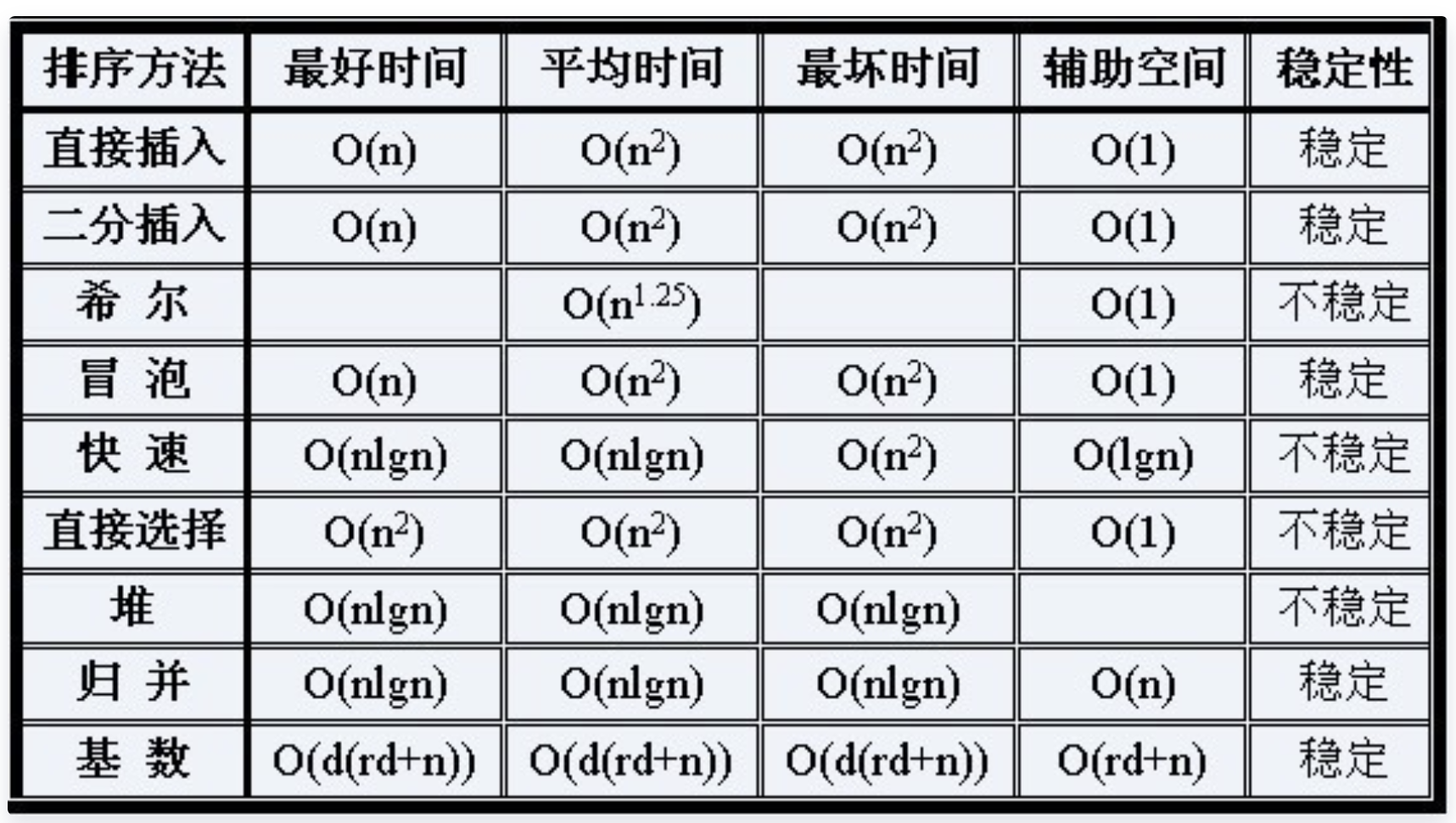
image-20220813161637101

3 空间复杂度

同时间复杂度不是统计程序运行的具体耗时，空间复杂度也不是统计程序运行的具体占用空间。空间复杂度是对一个算法在运行过程中临时占用存储空间大小的一个量度，同样反映的是一个趋势，用 S(n) 来定义。（时间复杂度为 **T (n)**）

空间复杂度比较常用的有：O(1)、O(n)、O(n²)

3.1 空间复杂度 O (1)

空间复杂度为 O (1) 的情况的示例代码与时间复杂度为 O (1) 的实例代码一致：

1
2
3
4
5
int i = 1;
int j = 2;
++i;
j++;
int m = i + j;

代码中的 i、j、m 所分配的空间都不随着处理数据量变化，因此它的空间复杂度 S(n) = O(1)

3.2 空间复杂度 O (n)

1
2
3
4
5
6
int j = 0;
int[] m = new int[n];
for (int i = 1; i <= n; ++i) {
   j = i;
   j++;
}

上述代码中，只有创建 int 数组分配空间时与 n 的大小有关，而 for 循环内没有再分配新的空间，因此，对应的空间复杂度为 S(n) = O(n)

3.3 空间复杂度 O (n²)

随着数据量的变化，内存消耗为平方变化，如：

1
2
3
4
5
6
int[][] arr = new int[n][n];
for (int i = 0; i < n; i++) {
    for (int j = 0; j < n; j++) {
        arr[i][j] = new Random().nextInt();
    }
}

以上二维数组中，当 n+1 的时候，arr 数组大小从 n² 变为了 (n+1)²，其它空间复杂度以此类。

总结

其实无论是时间复杂度还是空间复杂度，都是在考虑当 n 变化的时候时间或者空间会呈什么样的变化趋势，并最终确定时间和空间的上界问题。

  • 考虑时间复杂度的时候，我们简化为思考 n+1 的时候，循环次数如何变化，如果不变则 O(1)，线性则 O(n)，对数则 log(n)… 以此类推。也就是说把 n 当作问题规模，当 n 变化的时候，执行次数的变化呈现什么规律。
  • 考虑空间复杂度的时候，我们简化为思考 n+1 的时候，内存消耗的数量如何变化，如果不变则为 O(1)，线性则为 O(n)，平方则为 O(n²)… 以此类推。也就是说当 n 变化的时候，内存消耗的变化呈现什么规律。

引用